2024教师招聘面试说课稿：高中数学《复数的几何意义》-凯发旗舰厅真人

2024教师招聘面试说课稿：

高中数学《复数的几何意义》

一、说教材

教材分析的过程，就是教师不断提高业务素质和加深对教育理论理解的过程。

《复数的几何意义》是人教a版高中数学必修第二册第七章第一节的内容。复数的引入是中学阶段数系的又一次扩充，引入复数以后，这不仅可以使学生对于数的概念有一个初步的、完整的认知，也为进一步学习数学打下基础。通过本节课学习，使学生在问题情境中了解数系扩充的过程以及引入复数的必要性，体会人类理性思维在数系扩充中的作用。

基于以上教材地位和作用的分析，结合新课标理念，我确定本节课的教学目标为：

1.理解可以用复平面内的点或以原点为起点的向量来表示复数及它们之间的一一对应关系，掌握实轴、虚轴、模等概念及用向量的模来表示复数的模的方法;

2.通过复数几何意义的探究过程，提升数学抽象、逻辑推理及运算能力，并渗透数学模型意识;;

3.根据复数的代数形式，数形结合，多方位了解复数的几何意义，提高学生学习数学的兴趣。

课堂是教学的主阵地，提高课堂教学质量，优化教学过程，需要突出重点，突破难点。本节课的重点为理解复数的几何意义，根据复数的代数形式描出其对应的点及向量;难点是根据复数的代数形式描出其对应的点及向量。

二、说学情

教师不仅要对教材进行分析，还要对学生的情况有清晰明了的掌握，这样才能做到因材施教，有的放矢。接下来我将对学情进行分析。

对于该阶段的学生来说，他们已经学过代数、解析几何的相关知识，对本节课的探究，学生可以类比实数的几何意义自己探索复数的第一种几何意义，由于学生已经学过平面向量及其几何表示、坐标表示，理解复数还可以用平面向量来表示就比较容易了。但同时还要考虑学生对于知识的梳理和逻辑关联的组织能力上还存在一些欠缺，因此在本节课的学习中还需要一定的引导。

三、说教法学法

教师的教是为了学生更好的学，既要注重学生知识的获得，更要注重学生智力和能力的发展。在本课中我主要采用类比法、启发诱导法、讲练结合法等。本节课采用类比的教学方式，由实数用数轴上的点来表示，类比联想得到复数可用复平面上的点来表示，进而得到向量形式，由一维上升到二维，同时实现从“数”到“形”的转化。再类比平面向量的加减法，得到了复数加减法的几何意义，从而对复数有了新的认识。在学生对复数的几何意义的探究中还需要对学生进行一定的引导，有助于学生更好地接受本节课知识点，因此采用了启发诱导法。为了加强知识的及时巩固，我会采用讲练结合的方法。

四、说教学过程

基于以上分析，设计以下几个教学环节，下面我将从新课导入、新课讲授、巩固练习、小结作业四个部分重点阐述本堂课的教学过程。

(一)复习导入

课始之初，我会向学生提问：实数可以与数轴上的点一一对应，类比实数，复数能与什么一一对应呢?学生自由发言，我会引导学生进一步观察，探究复数的几何意义。由此导入新课。

(二)新课讲授

1.复平面

由于复平面的定义比较好理解，而且教材上描述非常详细，因此我会组织学生自主阅读这部分教材，并提问：什么是复平面?

3.共轭复数的定义

通过上述理论知识的学习后，我会给出教材上的例2，已知两个复数，求出其对应点和向量，并求出它们各自的模，然后比较模的大小。学生同桌合作完成。找学生回答，我给予评价。

接着让学生观察该例题的特点，不难发现例题中的两个复数实部相等，虚部互为相反数。从而我向学生讲授共轭复数的概念。

再次提出问题：如果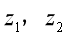是共轭复数，那么在复平面内它们对应的点有什么关系呢?

组织学生独立思考回答。不难得到共轭复数对应的两个点关于实轴x对称。

到此本节课知识点已经学习完毕。

(三)巩固练习

为了加强对本节课知识点的理解，我在课件上会出示两个复数，找两位学生在黑板上作出复平面，并在复平面中描出相应的点，其他学生自主完成。学生完成后我会跟全班学生一起对黑板上两位学生的板演进行共同评价。

(四)小结作业

课堂最后，我会让学生做一个小结，以系统梳理本节课的重要知识点及其学习体会。通过向学生提出这样一个问题“通过今天的学习，你们学到了什么?”，引导学生自己总结所学，我给予补充点评。

最后是作业布置。为了更好地巩固新知，加深对知识的印象及理解，我会布置适宜的课后习题第1-3题作为课下作业。并在下节课前完成批改，并从中总结相关问题，下节课课始做必要的修正与强调。

五、板书设计

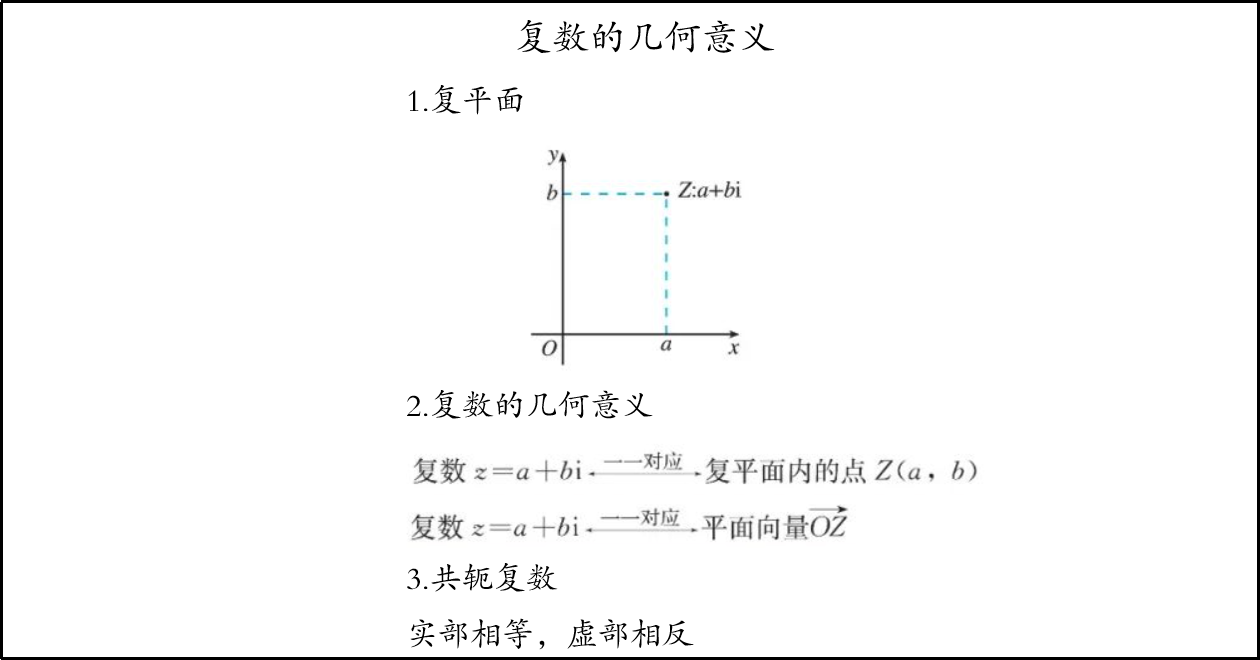
以上是我的板书设计，这样的板书简洁明了，条理有序，能够让学生较清晰地把握本节课的主要内容，并能够轻松地掌握主要知识点之间的逻辑顺序。我的说课到此结束，感谢各位评委老师!

2024年教师招聘官方微信客服

• 公告资讯
• 学习答疑
• 1对1指导
• 笔试资料
• 面试技巧
• 公开讲座

微信长按识别左侧二维码，添加

客服老师微信领取